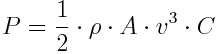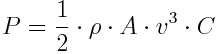in chapter 12, page 14, the core reading defines: which is called the radon-nikodyn derivative at T given F_t. However, this is never actually needed to work out the state price deflator, which simply uses: so my question is why do we need the first formula at all? thanks, gareth
GARETH i think the first firmuka is fir the proof construction. the A(t) in p14 is defined as r- n derivative * random discount factor , i think formula you quoted at bottom of your post is missing the random disocunt factor... i think the split of r -n dervative (via exponential addition) is needed because we are at time t and wish to price claim at T. so as the proof on 15 shows we have to break entire n (o,T) up into random n(t,T) and non random n (o,t) (as we know everything up to t) and then we are left with radon-nikodym derivative over (t,T)... and the rest of the manipulation leaves us with the stochastic discount factor over (t,T) and hence deflator over (t, T) so Expectation ( deflator(t,T) GIVEN Ft ) under P reduces to usual Q risk neutral formula over t,T) please correct me of i am wrong, but proving equalivalece of deflator and risk neutral approach at time 0 of a claim at T would not require any split of r-n derivative.. im sorry, gareth, but i havent yet learned the maths equation editor so as usual my symbology is poor also thank you very much for looking over question 3 in sept 05 paper (my thanks extends to mtm, ollie and others on this forum who commented)..it was a relief to know i wasnt the only one who was confused by the "TYPO"!!! regards
oops i did indeed miss a discount factor. i still don't think the eta(t,T) is needed for the proof. Here's my proof of it:
gareth youve done the proof the other way round - from risk neutral pricing q to defaltor approach under p - which looks very much nicer! i see you got an e(t) and a e(T) representing r - n derivatives / change of measure factors up to time t and T repectively. your approach is consitent with baxter and rennie p 67 -68 for evaluating conditional expections/given Ft under measures P and Q - " we need the amount of change of measure from t to T - which is just e(T) / e(t) - That is change up to time T with change up to time t removed" (b & r 68 using t/T instead of s/t) - this is where the n (t,T) must come from in the core reading way - representing measure change t to T....
