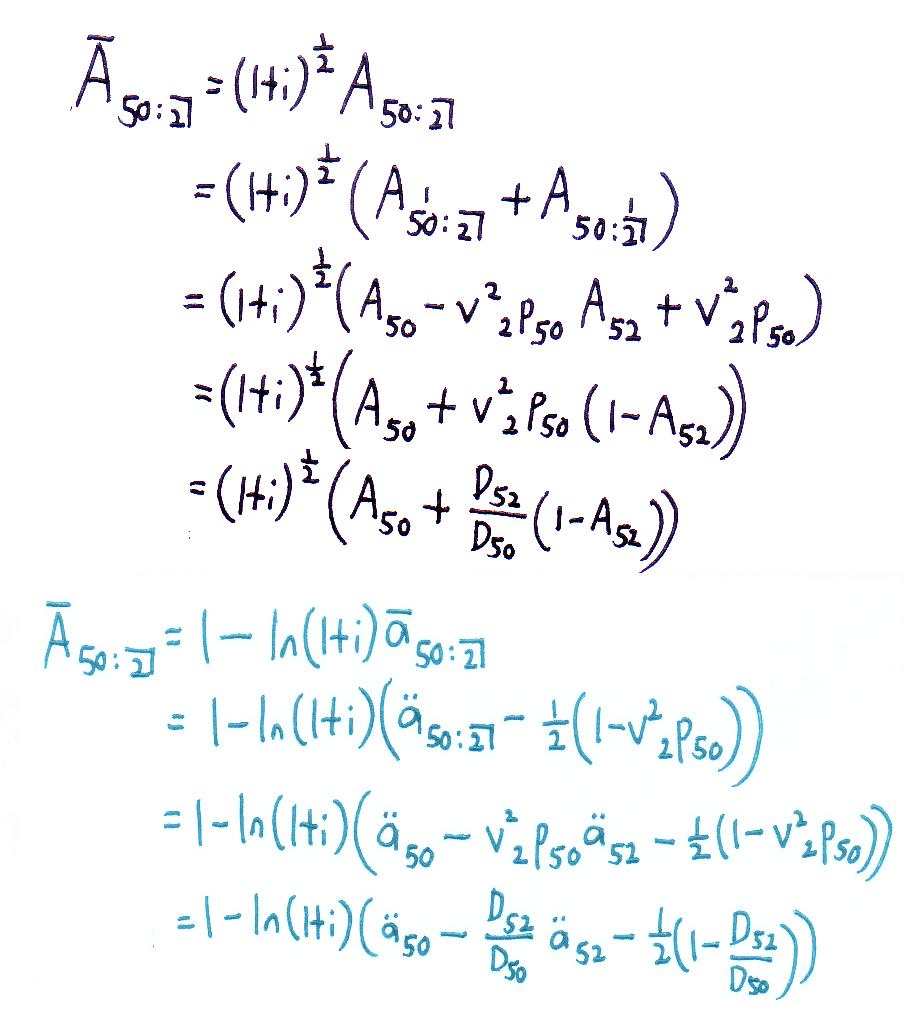Is this correct way to find value of endowment assurance payable immediately on death with x=50, n=2, i=.04 ? Will this approach get credit in exam?
The method above is the one I was taught by my Prof to solve this kind of question in general. However, your method that involves bringing in the annuity function should be acceptable and in fact is required in the Joint Life calculations because there is no table for joint life assurances under any basis.
@NewStudent - question 8 at the end of chapter 18 asks for the exact value of the assurance, if you've got a constant force of mortality between ages. Step 3 in your workings uses an approximation to convert the annuity-due to a continuously payable annuity, so you've got an approximate rather than an exact value here. This means that your approach is not likely to get credit in the exam if you've specifically been asked for an exact value. @Calm - your first approach (in black) doesn't quite work. This is because the survival benefit under this endowment assurance will always be paid at time 2. Applying the \( (1+i)^{\frac{1}{2}} \) to the whole \( \require{enclose} A_{50:{\enclose{actuarial}{2}}} \) means that you're bringing both the death and survival benefits forward by half a year. The correct approximation for an endowment assurance is \( (1+i)^{\frac{1}{2}} \require{enclose} A^1_{50:{\enclose{actuarial}{2}}} + \frac{D_{52}}{D_{50}} \) , i.e. you need to split the death and survival benefits up because the timing of survival benefits is always the same.
Thanks for pointing that out, didn't realise doing the steps in that order was effectively making the pure endowment component "continuously payable" which isn't true.
