CM2 BROWNIAN MOTION

[Adithyan]

W(0)" role="presentation" style="display: inline; line-height: normal; overflow-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; padding: 0px; margin: 0px; position: relative;">W(0)W(0) is just a constant so it has zero variance and an expected value of, well, W(0)" role="presentation" style="display: inline; line-height: normal; overflow-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; padding: 0px; margin: 0px; position: relative;">W(0)W(0).
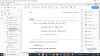
σB(t)" role="presentation" style="display: inline; line-height: normal; overflow-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; padding: 0px; margin: 0px; position: relative;">σB(t)σB(t) is a constant multiple of standard Brownian motion (which we know has a N(0,t)" role="presentation" style="display: inline; line-height: normal; overflow-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; padding: 0px; margin: 0px; position: relative;">N(0,t)N(0,t) distribution. Therefore σB(t)" role="presentation" style="display: inline; line-height: normal; overflow-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; padding: 0px; margin: 0px; position: relative;">σB(t)σB(t) has an expected value of zero and a variance of σ2t" role="presentation" style="display: inline; line-height: normal; overflow-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; padding: 0px; margin: 0px; position: relative;">σ2tσ2t (are you happy about this bit?).
μ(t)" role="presentation" style="display: inline; line-height: normal; overflow-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; padding: 0px; margin: 0px; position: relative;">μ(t)μ(t) is a deterministic function in t" role="presentation" style="display: inline; line-height: normal; overflow-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; padding: 0px; margin: 0px; position: relative;">tt so it has zero variance and an expected value of μ(t)" role="presentation" style="display: inline; line-height: normal; overflow-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; padding: 0px; margin: 0px; position: relative;">μ(t)μ(t).

This means that log⁡S(t)" role="presentation" style="display: inline; line-height: normal; overflow-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; padding: 0px; margin: 0px; position: relative;">logS(t)log⁡S(t) must be normally distributed, with mean W(0)+μ(t)" role="presentation" style="display: inline; line-height: normal; overflow-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; padding: 0px; margin: 0px; position: relative;">W(0)+μ(t)W(0)+μ(t) and variance σ2t" role="presentation" style="display: inline; line-height: normal; overflow-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; padding: 0px; margin: 0px; position: relative;">σ2tσ2t.

 

[Anna Bishop]

Adithyan - can you take a photo of your workings or do a 'print screen' and then upload it to the forum as an image file (jpeg, png, gif)?
Anna

 

[Adithyan]

Can you help me understand why sigma*B(t) has N(0, sigma^2 * t) distribution?

As per the 2nd file, I would like to know why there is no covariance term?

Var(a+b) = var(a)+var(b)+cov(a,b)

 

[Anna Bishop]

Yes, sure!

First off, we need to recognise that B(t) can be written as B(t) - B(0), since B(0) = 0.

Now B(t) = B(t) - B(0) is a standard Brownian Motion increment. Standard Brownian Motion increments:

a) are normally distributed
b) have a mean of 0
c) have a variance equal to the time lag, which is t - 0 = t.

So B(t) has a N(0,t) distribution.

Now we need to recall properties of normally distributed random variables. Say X is N(a, b). Then:

• cX is N(ca, c^2 b)
• X + c is N(a + c, b)
• exp(X) is logN(a, b)

To see why the first bullet holds, work out the mean and the variance.

E[cX] = c E[X] = ca
var[cX] = c^2 var[X] = c^2 b

To see why the second bullet holds, work out the mean and the variance.

E[X + c] = E[X] + c = a + c
var[X + c] = var[X] = b (note that additive constants do not alter the variance).

To see why the third bullet holds, we use the rule that:

If log Y is N(a, b) then Y is logN(a,b).
Equivalently, if X is N(a, b) then exp(X) is logN(a, b).
This follows by setting X = log Y so that Y = exp(X).

Your question is a case of the first bullet.
sigma B(t) is N(0, sigma^2 t)

Re the other query, you are right to say that usually:

var(a + b) = var(a) + var(b) + 2cov(a, b).

When a and b are independent, as is the case in the picture, the covariance term disappears as a and b do not relate to each other, and we are left with:

var(a + b) = var(a) + var(b)

Hope this all helps
Anna

 

[Adithyan]

Yes, sure!

First off, we need to recognise that B(t) can be written as B(t) - B(0), since B(0) = 0.

Now B(t) = B(t) - B(0) is a standard Brownian Motion increment. Standard Brownian Motion increments:

a) are normally distributed
b) have a mean of 0
c) have a variance equal to the time lag, which is t - 0 = t.

So B(t) has a N(0,t) distribution.

Now we need to recall properties of normally distributed random variables. Say X is N(a, b). Then:

• cX is N(a, c^2 b)
• X + c is N(a + c, b)
• exp(X) is logN(a, b)

To see why the first bullet holds, work out the mean and the variance.

E[cX] = c E[X] = ca
var[cX] = c^2 var[X] = c^2 b

To see why the second bullet holds, work out the mean and the variance.

E[X + c] = E[X] + c = a + c
var[X + c] = var[X] = b (note that additive constants do not alter the variance).

To see why the third bullet holds, we use the rule that:

If log Y is N(a, b) then Y is logN(a,b).
Equivalently, if X is N(a, b) then exp(X) is logN(a, b).
This follows by setting X = log Y so that Y = exp(X).

Your question is a case of the first bullet.
sigma B(t) is N(0, sigma^2 t)

Re the other query, you are right to say that usually:

var(a + b) = var(a) + var(b) + 2cov(a, b).

When a and b are independent, as is the case in the picture, the covariance term disappears as a and b do not relate to each other, and we are left with:

var(a + b) = var(a) + var(b)

Hope this all helps
Anna

Can you tell my why

• cX is N(a, c^2 b) and not N(ca, c^2 b)?

 

[Anna Bishop]

My mistake Adithyan - I've edited (corrected) it in the above post.